Transformada Rápida de Fourier: Fundamentos y Aplicaciones

Introducción a la Transformada Rápida de Fourier (FFT)

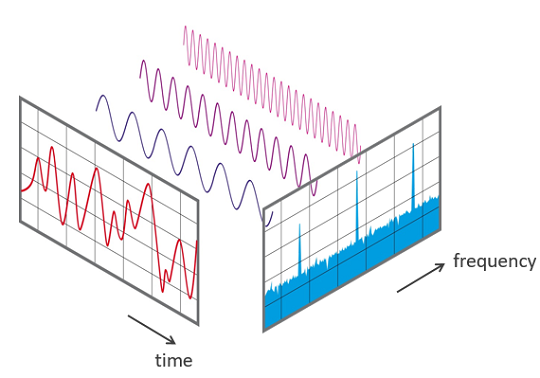
La Transformada Rápida de Fourier (FFT por sus siglas en inglés, Fast Fourier Transform) es uno de los algoritmos más importantes y utilizados en la computación científica y el procesamiento de señales. Desempeña un papel esencial en una variedad de campos como la física, la ingeniería eléctrica, la computación, y más recientemente en áreas como la biomedicina y la inteligencia artificial. La FFT permite la transformación de una señal desde el dominio temporal al dominio frecuencial de manera eficiente, lo que proporciona una forma rápida y precisa de analizar la frecuencia de una señal.

Este artículo explora los fundamentos matemáticos de la FFT, su historia, su desarrollo y las aplicaciones prácticas en diversos campos. También abordaremos su importancia y cómo ha transformado diferentes industrias y disciplinas académicas.

Historia y Desarrollo de la FFT

El concepto de Transformada de Fourier fue introducido por el matemático francés Joseph Fourier a principios del siglo XIX. Fourier propuso que cualquier función periódica podría ser representada como una suma infinita de funciones seno y coseno, lo que hoy conocemos como series de Fourier. Sin embargo, la transformada de Fourier discreta (DFT, Discrete Fourier Transform) es la versión que se utiliza en la computación digital para convertir una señal discreta en el tiempo en una representación en el dominio de la frecuencia.

El desarrollo de la FFT como la conocemos fue presentado en 1965 por los matemáticos James Cooley y John Tukey, quienes encontraron una manera de reducir el costo computacional de la DFT de $O(N^2)$ a $O(N \log N)$, donde $N$ es el número de puntos de la señal. Este avance fue revolucionario, ya que permitió el análisis frecuencial de señales mucho más largas en un tiempo razonable, allanando el camino para aplicaciones en procesamiento de señales, imagen digital, comunicaciones y muchos otros campos.

Fundamentos Matemáticos

La Transformada de Fourier Discreta (DFT)

Para entender la FFT, es importante comprender primero la Transformada de Fourier Discreta. La DFT se utiliza para convertir una secuencia finita de puntos en una representación frecuencial, que nos dice qué componentes de frecuencia están presentes en la señal original.

Matemáticamente, la DFT de una secuencia $x[n]$ de longitud $N$ se define como:

$$X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-i 2\pi kn / N}$$

donde:

• $n$ es el índice de tiempo,
• $k$ es el índice de frecuencia,
• $i$ es la unidad imaginaria ($i = \sqrt{-1}$),
• $x[n]$ es la secuencia de entrada,
• $X[k]$ es la representación de frecuencia.

Este cálculo tiene una complejidad de $O(N^2)$ porque requiere $N$ multiplicaciones para cada uno de los $N$ puntos de la señal, lo cual se vuelve computacionalmente prohibitivo para señales largas.

La Transformada Rápida de Fourier (FFT)

La FFT es una implementación optimizada de la DFT que reduce el número de operaciones requeridas utilizando un algoritmo basado en la descomposición recursiva de la señal original. El método más común es el algoritmo de Cooley-Tukey, que divide la señal en partes más pequeñas, realiza la DFT en cada parte y luego combina los resultados.

Para un número de puntos $N$ que es una potencia de 2, el algoritmo divide la señal en dos partes: una compuesta de los índices pares y otra de los índices impares. Este proceso de división continua hasta que se alcanza el tamaño mínimo (normalmente $N=2$), lo que permite un cálculo rápido y eficiente.

$$X[k] = \sum_{n=0}^{N/2-1} \left[ x[2n] \cdot e^{-i2\pi k \frac{2n}{N}} + x[2n+1] \cdot e^{-i2\pi k \frac{2n+1}{N}} \right]$$

La FFT reduce el número de operaciones a $O(N \log N)$, lo que significa que puede manejar señales mucho más grandes de manera eficiente.

Aplicaciones de la FFT

1. Procesamiento de Señales

Una de las aplicaciones más conocidas de la FFT es en el procesamiento de señales, donde se utiliza para analizar las frecuencias que componen una señal. Por ejemplo, en audio, la FFT se utiliza para convertir una señal de sonido en el dominio del tiempo en el dominio de la frecuencia, lo que permite identificar las distintas frecuencias (notas) presentes en el sonido.

• Análisis de Espectro: La FFT se utiliza en análisis de espectro para descomponer una señal compleja en sus componentes de frecuencia. Esto es crucial en el análisis de audio, radar, comunicaciones y vibraciones mecánicas.
• Compresión de Audio y Video: La FFT también es fundamental en técnicas de compresión de datos como el formato MP3 y la Transformada de Coseno Discreta (DCT) que se utiliza en la compresión de imágenes JPEG y videos MPEG.

2. Procesamiento de Imágenes

En el campo del procesamiento de imágenes, la FFT se utiliza para realizar operaciones como el filtrado en el dominio de la frecuencia. Por ejemplo, se pueden suprimir ciertas frecuencias no deseadas (como el ruido) para mejorar la calidad de una imagen.

• Filtrado de Imágenes: La FFT permite aplicar filtros en el dominio de la frecuencia, lo cual es útil para eliminar ruido o mejorar ciertas características de una imagen.
• Reconocimiento de Patrones: En la visión artificial, la FFT puede ayudar a encontrar características repetitivas o patrones dentro de una imagen, lo que es esencial en aplicaciones como el reconocimiento de caras y objetos.

3. Comunicaciones

La FFT es un componente esencial en muchos sistemas de comunicaciones digitales, donde se utiliza para procesar señales modulares como las de OFDM (Multiplexación por División de Frecuencia Ortogonal), que es la base de muchas tecnologías modernas de comunicación como el Wi-Fi, 4G LTE, y 5G.

• Modulación y Demodulación: La FFT se utiliza para convertir señales del dominio temporal al dominio frecuencial en sistemas de modulación digital.
• Filtrado de Banda: En los sistemas de comunicaciones, es común filtrar ciertas bandas de frecuencia para evitar interferencias y mejorar la calidad de la señal.

4. Física y Simulaciones Científicas

La FFT también se utiliza en simulaciones científicas en física y matemáticas, donde es necesario resolver ecuaciones diferenciales parciales o analizar la evolución de sistemas dinámicos.

• Simulaciones de Campos Electromagnéticos: En electromagnetismo, la FFT se utiliza para transformar campos eléctricos y magnéticos al dominio de la frecuencia, lo cual simplifica el análisis y la simulación.
• Mecánica Cuántica: En física cuántica, se utiliza la FFT para analizar la evolución temporal de funciones de onda.

5. Medicina e Imagenología

En la medicina, la FFT juega un papel importante en la creación y análisis de imágenes médicas, como en la tomografía computarizada (TC) y la resonancia magnética (RM).

• Análisis de EEG: Los electroencefalogramas (EEG) son registros de la actividad eléctrica del cerebro que se analizan utilizando la FFT para identificar patrones relacionados con diversas condiciones médicas como epilepsia o trastornos del sueño.
• Imagenología Médica: En la RM, la FFT se utiliza para transformar los datos del dominio de la frecuencia en imágenes espaciales, permitiendo a los médicos visualizar tejidos internos con gran precisión.

Variaciones y Extensiones de la FFT

FFT Rápida Multidimensional

La FFT se puede extender a múltiples dimensiones. En lugar de solo transformar datos unidimensionales (como en señales de audio), se puede aplicar la FFT en imágenes (dos dimensiones) o en volúmenes (tres dimensiones), lo cual es útil en aplicaciones como la tomografía computarizada y la reconstrucción de imágenes 3D.

FFT en Hardware

Debido a la necesidad de realizar cálculos rápidos y eficientes, muchas implementaciones de FFT se llevan a cabo en hardware dedicado, como los procesadores digitales de señales (DSPs) y las Unidades de Procesamiento Gráfico (GPUs). Estas plataformas permiten que las operaciones de FFT se realicen en paralelo, lo que aumenta significativamente la velocidad de procesamiento.

FFT Paralela

Con la evolución de la computación de alto rendimiento (HPC), se han desarrollado versiones paralelas de la FFT para ejecutarse en múltiples procesadores simultáneamente. Esto es especialmente útil en aplicaciones de simulación científica donde se deben procesar grandes volúmenes de datos en tiempo real.

Desafíos y Limitaciones

Eficiencia

Aunque la FFT es extremadamente eficiente comparada con la DFT directa, tiene ciertas limitaciones cuando el número de muestras $N$ no es una potencia de 2, lo cual puede requerir técnicas adicionales para ajustar el tamaño de la señal.

Artefactos en el Dominio de la Frecuencia

En algunas aplicaciones, la FFT puede introducir artefactos no deseados debido a la suposición implícita de periodicidad en la señal. Para mitigar este problema, se suelen utilizar técnicas como ventanado (windowing) para suavizar las transiciones en los extremos de la señal.

Ruido y Señales No Estacionarias

La FFT asume que la señal es estacionaria (es decir, que no cambia en el tiempo), lo cual no siempre es cierto en la práctica. Para señales no estacionarias, como señales de audio o datos financieros, se utilizan variantes de la FFT, como la Transformada de Fourier de Ventana Móvil (STFT), que permite analizar pequeñas porciones de la señal a la vez.

Conclusión

La Transformada Rápida de Fourier ha sido una herramienta clave en el análisis de señales y ha permitido importantes avances en una variedad de campos, desde las telecomunicaciones hasta la medicina. Su capacidad para descomponer señales en componentes frecuenciales de manera eficiente ha revolucionado la forma en que analizamos y procesamos datos en el mundo digital. Sin embargo, a pesar de sus muchas ventajas, la FFT tiene limitaciones que requieren enfoques adicionales en aplicaciones más complejas.

En un mundo donde el procesamiento de grandes volúmenes de datos es esencial, la FFT seguirá siendo una de las herramientas matemáticas más importantes y utilizadas en la ingeniería y la ciencia.

Más Informaciones

La Transformada Rápida de Fourier (FFT por sus siglas en inglés, Fast Fourier Transform) es un algoritmo crucial en el campo del procesamiento de señales y la computación numérica. Se utiliza para transformar una señal desde el dominio del tiempo al dominio de la frecuencia, lo que permite analizar y procesar eficientemente señales en diferentes aplicaciones, como procesamiento de imágenes, comunicaciones inalámbricas, procesamiento de audio y vídeo, entre otros.

Desarrollada originalmente por el matemático estadounidense John Tukey a finales de la década de 1950, la FFT es una versión eficiente de la Transformada Discreta de Fourier (DFT), que calcula la descomposición de una señal en sus componentes de frecuencia. La DFT es fundamental en el análisis de señales, pero su cálculo directo puede ser computacionalmente costoso, especialmente para señales de gran tamaño.

La FFT reduce drásticamente la cantidad de operaciones necesarias para calcular la DFT al explotar la estructura periódica de las funciones sinusoidales y cosinusoidales. En lugar de realizar N^2 operaciones (donde N es el número de muestras en la señal), como lo haría el cálculo directo de la DFT, la FFT realiza solo alrededor de N log N operaciones, lo que la hace significativamente más eficiente, especialmente para señales largas.

Existen varias formas de implementar la FFT, siendo el algoritmo Cooley-Tukey uno de los más conocidos. Este algoritmo divide recursivamente la DFT en DFT más pequeñas, lo que reduce la complejidad computacional. Además, la FFT puede aprovechar la simetría de las señales de entrada para lograr una mayor eficiencia. Por ejemplo, si la señal es real y no compleja, aproximadamente la mitad de los cálculos se pueden evitar utilizando propiedades de simetría.

La FFT ha revolucionado numerosos campos, incluida la ingeniería de señales, la física, la astronomía, la ingeniería eléctrica y la música, entre otros. En el procesamiento de imágenes, por ejemplo, la FFT se utiliza para aplicar filtros de frecuencia, mejorar la compresión de imágenes y realizar transformaciones de dominio, como la transformación de Fourier discreta bidimensional (2D).

En aplicaciones de comunicaciones, la FFT es esencial para la modulación y demodulación de señales, así como para la multiplexación por división de frecuencia ortogonal (OFDM), una técnica utilizada en estándares de comunicación inalámbrica como Wi-Fi y LTE.

En el ámbito del procesamiento de audio y música, la FFT se utiliza para la síntesis y análisis de sonido, la cancelación de ruido, la equalización y la detección de tonos, entre otras aplicaciones.

Aunque la FFT es extremadamente poderosa y versátil, su implementación eficiente sigue siendo un área de investigación activa. Se han propuesto numerosas variantes y mejoras de la FFT para adaptarse a diferentes tipos de señales y aprovechar las características específicas de las arquitecturas de hardware modernas, como las GPU y las FPGA.

En resumen, la Transformada Rápida de Fourier es una herramienta fundamental en el procesamiento de señales, que ha tenido un profundo impacto en una amplia gama de campos científicos y tecnológicos, permitiendo el análisis y procesamiento eficiente de señales en el dominio de la frecuencia. Su eficiencia y versatilidad la convierten en un componente esencial en numerosas aplicaciones modernas.