Los polígonos son figuras geométricas que pueden clasificarse según la cantidad de lados que posean. Uno de los tipos más interesantes de polígonos son los polígonos de lados iguales, denominados polígonos regulares. Dentro de esta categoría, se encuentra un tipo particularmente notable conocido como el polígono de lados iguales y ángulos iguales, o simplemente, el polígono regular. Entre los polígonos regulares, uno de los más intrigantes es el polígono de lados iguales y ángulos iguales, comúnmente denominado polígono equilátero.
El polígono equilátero, también conocido como polígono equiangulado, se caracteriza por tener todos sus lados de igual longitud y todos sus ángulos internos de igual medida. Este tipo de polígono presenta propiedades únicas que lo distinguen y lo hacen objeto de estudio en diversas ramas de la geometría y la matemática.
Una de las características más destacadas del polígono equilátero es su simetría. Dado que todos sus lados son de igual longitud y todos sus ángulos son iguales, el polígono equilátero exhibe múltiples ejes de simetría. En particular, un polígono equilátero posee tantos ejes de simetría como lados, lo que significa que cada lado es un eje de simetría. Esta propiedad lo convierte en una figura geométrica especialmente interesante en el estudio de la simetría y la geometría euclidiana.
Otra propiedad notable del polígono equilátero es su relación con el círculo. Al inscribir un polígono equilátero en un círculo, es posible demostrar que el centro del círculo coincide con el centro del polígono y que todos los vértices del polígono equidistan del centro del círculo. Esta característica es fundamental para entender la relación entre los polígonos regulares y los círculos, y es un tema importante en la geometría elemental y avanzada.
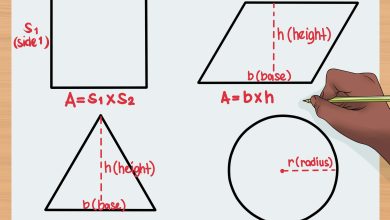
Además de su simetría y su relación con el círculo, el polígono equilátero también posee propiedades interesantes relacionadas con su área y su perímetro. Dado que todos sus lados son iguales, calcular el perímetro del polígono equilátero es tan simple como multiplicar la longitud de uno de sus lados por la cantidad de lados que tiene el polígono. Del mismo modo, el área del polígono equilátero puede calcularse utilizando fórmulas específicas que dependen de la longitud de sus lados. Estas propiedades hacen que el polígono equilátero sea objeto de estudio en problemas de geometría y matemáticas aplicadas.
En el contexto de la geometría euclidiana, el polígono equilátero también desempeña un papel importante en la construcción de figuras más complejas. Por ejemplo, al combinar varios polígonos equiláteros, es posible construir poliedros regulares, como el tetraedro, el octaedro y el icosaedro, entre otros. Estas construcciones tienen aplicaciones en diversas áreas, incluida la geometría, la arquitectura y la ingeniería.
En resumen, el polígono equilátero es una figura geométrica fascinante que se caracteriza por tener todos sus lados de igual longitud y todos sus ángulos de igual medida. Sus propiedades únicas, como su simetría, su relación con el círculo y sus características relacionadas con el área y el perímetro, lo convierten en un objeto de estudio importante en la geometría y las matemáticas. Además, su papel en la construcción de figuras más complejas lo hace relevante en diversos campos, desde la arquitectura hasta la ingeniería.
Más Informaciones
Por supuesto, profundicemos más en las características y propiedades del polígono equilátero.
Una de las propiedades más notables del polígono equilátero es su capacidad para formar patrones regulares y simétricos cuando se disponen en conjuntos más grandes. Por ejemplo, al unir varios polígonos equiláteros en un patrón hexagonal, se crea una estructura conocida como panal de abejas, que se encuentra comúnmente en la naturaleza como la disposición de las celdas en una colmena. Esta disposición hexagonal maximiza el uso del espacio y minimiza la cantidad de material necesario para construir la estructura, lo que la convierte en una solución eficiente desde el punto de vista energético y estructural.
Otra característica interesante del polígono equilátero es su relación con otras figuras geométricas. Por ejemplo, al unir los centros de los lados de un polígono equilátero se forma un triángulo equilátero dentro del polígono original. Este triángulo equilátero es conocido como el triángulo medial del polígono equilátero y comparte muchas propiedades con el polígono original, como la igualdad de lados y ángulos.
Además, el polígono equilátero es fundamental en la construcción de otros polígonos regulares más complejos. Por ejemplo, al unir los vértices de un polígono equilátero se puede formar un polígono regular de mayor cantidad de lados, como un hexágono, un octógono, o incluso un polígono de 12 lados. Este proceso de construcción se basa en la división del círculo en partes iguales utilizando los ángulos y lados del polígono equilátero como guía.
En términos de su relación con el círculo, el polígono equilátero también es importante en la geometría analítica. Por ejemplo, al considerar un círculo de radio unitario, se puede demostrar que la longitud de un lado de un polígono equilátero inscrito en ese círculo es igual a la unidad, lo que facilita cálculos trigonométricos y algebraicos relacionados con el polígono.
Otra aplicación interesante del polígono equilátero se encuentra en el campo de la computación gráfica y la geometría computacional. Los polígonos equiláteros son fundamentales en la creación de gráficos por computadora, ya que se utilizan como bloques de construcción para representar formas más complejas en entornos virtuales tridimensionales. Al dividir una superficie en polígonos equiláteros más pequeños, se pueden aproximar formas y superficies con mayor precisión, lo que permite crear modelos virtuales de objetos reales con un alto nivel de detalle y realismo.
En resumen, el polígono equilátero es una figura geométrica fascinante que tiene una amplia variedad de aplicaciones y propiedades interesantes. Desde su capacidad para formar patrones regulares y simétricos hasta su importancia en la construcción de otros polígonos regulares y su papel en la geometría analítica y computacional, el polígono equilátero sigue siendo objeto de estudio y exploración en diversos campos de la matemática y la ciencia.