Media Aritmética: Características y Aplicaciones
Introducción
La media aritmética, también conocida simplemente como promedio, es una de las medidas estadísticas más utilizadas para describir un conjunto de datos. Su simplicidad y aplicabilidad la convierten en una herramienta esencial en diversos campos, desde la economía y la educación hasta la ingeniería y las ciencias sociales. En este artículo, exploraremos en profundidad las características de la media aritmética, su cálculo, ventajas, limitaciones, y las múltiples aplicaciones que tiene en la vida diaria y en disciplinas especializadas.
Definición y Cálculo de la Media Aritmética
Definición
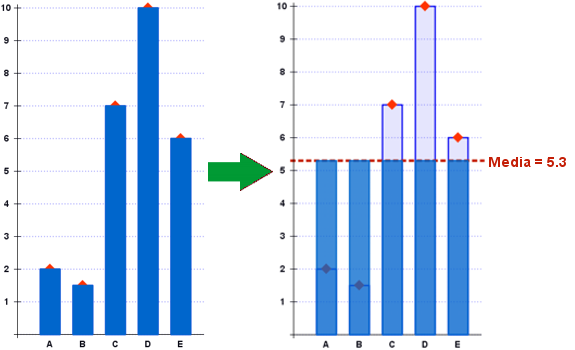
La media aritmética es un valor que se obtiene al sumar todos los números en un conjunto de datos y luego dividir esa suma por la cantidad de números en el conjunto. En matemáticas, se expresa de la siguiente manera:
donde son los valores individuales del conjunto de datos y es el número total de valores.
Ejemplo de Cálculo
Consideremos un conjunto de datos: 5, 10, 15, 20, 25. La media aritmética se calcula de la siguiente manera:
Esto significa que el promedio de los números en este conjunto de datos es 15.
Características de la Media Aritmética
Propiedades Matemáticas
- Simplicidad: La media aritmética es fácil de calcular y comprender, lo que la convierte en una herramienta accesible para todos.
- Sensibilidad a Valores Extremos: La media aritmética es sensible a los valores atípicos o extremos, lo que puede distorsionar el valor promedio en conjuntos de datos con distribuciones asimétricas.
- Equidad: En un conjunto de datos, la media aritmética distribuye el valor total equitativamente entre todos los datos, representando un «punto de equilibrio».
Relación con Otras Medidas de Tendencia Central
La media aritmética es una de las varias medidas de tendencia central, junto con la mediana y la moda. A diferencia de la mediana, que mide el punto medio de un conjunto de datos, y la moda, que es el valor más frecuente, la media aritmética considera todos los valores en el conjunto de datos.
Uso en Diferentes Distribuciones
La media aritmética es más efectiva en distribuciones simétricas, donde los valores están equilibrados alrededor del centro. En distribuciones sesgadas, la media puede no ser representativa del «centro» del conjunto de datos.
Ventajas de la Media Aritmética
Representación Simple y Clara
Una de las mayores ventajas de la media aritmética es su simplicidad y claridad. Es fácil de interpretar y proporciona una visión general rápida del conjunto de datos.
Uso Universal
La media aritmética es una herramienta universal utilizada en prácticamente todos los campos, desde la ciencia hasta los negocios. Es fundamental para el análisis de datos y la toma de decisiones basada en estadísticas.
Capacidad de Cálculo Rápido
Con la tecnología actual, calcular la media aritmética de grandes conjuntos de datos es rápido y eficiente, lo que permite a las organizaciones analizar y procesar datos a gran escala.
Limitaciones de la Media Aritmética
Sensibilidad a Valores Extremos
Como se mencionó anteriormente, la media aritmética es altamente sensible a los valores extremos o atípicos. En conjuntos de datos con una o varias observaciones extremadamente altas o bajas, la media puede no reflejar adecuadamente el comportamiento general del conjunto.
No Considera la Distribución de los Datos
La media aritmética no proporciona información sobre la dispersión o la variabilidad de los datos. Dos conjuntos de datos diferentes pueden tener la misma media aritmética, pero comportarse de manera completamente diferente.
Limitaciones en Datos Cualitativos
La media aritmética solo es aplicable a datos cuantitativos. No puede ser utilizada para describir conjuntos de datos cualitativos, donde los valores representan categorías o clases.
Aplicaciones de la Media Aritmética
Economía y Finanzas
En economía, la media aritmética se utiliza para calcular promedios como el ingreso per cápita, que es fundamental para medir el nivel de vida en diferentes regiones. En finanzas, se emplea para calcular el rendimiento promedio de inversiones a lo largo del tiempo.
Educación
En el ámbito educativo, la media aritmética se utiliza para calcular el promedio de calificaciones de los estudiantes, lo que permite evaluar su rendimiento general en un curso o durante un año académico.
Ciencias Sociales
En las ciencias sociales, la media aritmética se emplea para analizar datos de encuestas y estudios, como el ingreso promedio, la edad promedio, o el nivel promedio de satisfacción de una población.
Ingeniería y Tecnología
En ingeniería, la media aritmética es crucial para la estimación de parámetros como la vida útil promedio de un componente, el tiempo medio entre fallos (MTBF), y otros indicadores de rendimiento.
Estadísticas y Análisis de Datos
La media aritmética es una de las primeras herramientas utilizadas en el análisis de datos estadísticos. Es la base para más análisis complejos como la regresión lineal, la evaluación de hipótesis, y la creación de modelos predictivos.
Casos Especiales en el Uso de la Media Aritmética
Media Aritmética Ponderada
En algunos casos, ciertos valores en un conjunto de datos pueden tener más importancia que otros. En estos casos, se utiliza la media aritmética ponderada, donde cada valor es multiplicado por un peso que refleja su importancia antes de calcular la media.
Esta fórmula es especialmente útil en finanzas para calcular el rendimiento de una cartera de inversiones, donde cada activo tiene un peso diferente basado en su proporción en la cartera.
Media Aritmética Geométrica
En algunas situaciones, como en el cálculo del crecimiento medio de una inversión a lo largo del tiempo, la media geométrica es más apropiada. Aunque la media geométrica no es lo mismo que la media aritmética, se menciona aquí como una alternativa cuando la media aritmética puede no ser adecuada.
Ejemplos Prácticos de la Media Aritmética en Diferentes Disciplinas
Ejemplo en Economía
Consideremos un análisis de los ingresos anuales en una comunidad. Si se desea calcular el ingreso promedio, se suman todos los ingresos y se divide por el número de personas. Sin embargo, si hay una persona con un ingreso extremadamente alto, la media aritmética podría no representar adecuadamente la mayoría de los ingresos.
Ejemplo en Educación
Supongamos que un profesor quiere calcular el promedio de calificaciones de sus estudiantes en un examen. Si la mayoría de los estudiantes tiene una puntuación entre 70 y 90, pero uno tiene una puntuación de 30, la media aritmética dará un resultado más bajo de lo que la mayoría de los estudiantes obtuvo realmente.
Ejemplo en Finanzas
En finanzas, si se quiere calcular el rendimiento promedio de un fondo de inversión durante varios años, la media aritmética puede ser utilizada. Sin embargo, es importante considerar si los rendimientos son consistentes o si hay años con rendimientos extremadamente bajos o altos.
Comparación de la Media Aritmética con Otras Medidas de Tendencia Central
Media vs. Mediana
La mediana es el valor que se encuentra en el centro de un conjunto de datos cuando estos están ordenados. A diferencia de la media, la mediana no se ve afectada por valores extremos, lo que la hace más representativa en distribuciones sesgadas.
Media vs. Moda
La moda es el valor más frecuente en un conjunto de datos. En conjuntos de datos con distribuciones multimodales (con varias modas), la moda puede ser más representativa que la media o la mediana.
Importancia de la Media Aritmética en la Toma de Decisiones
Decisiones Basadas en Datos
La media aritmética es fundamental para la toma de decisiones en entornos basados en datos. Proporciona una forma rápida y eficiente de resumir un gran conjunto de datos en un solo valor representativo.
Análisis Comparativo
La media aritmética permite realizar comparaciones entre diferentes conjuntos de datos. Por ejemplo, se puede comparar el ingreso promedio de dos regiones para determinar cuál tiene un nivel de vida más alto.
Uso en Evaluaciones de Desempeño
En las empresas, la media aritmética se utiliza para evaluar el desempeño promedio de empleados, departamentos, o productos, facilitando la identificación de áreas que requieren mejoras o que están superando las expectativas.
Herramientas para el Cálculo de la Media Aritmética
Software Estadístico
Existen numerosos programas de software estadístico, como SPSS, R, y Python (con bibliotecas como Pandas y NumPy), que permiten calcular fácilmente la media aritmética, incluso en grandes conjuntos de datos.
Hojas de Cálculo
Las hojas de cálculo, como Microsoft Excel o Google Sheets, ofrecen funciones integradas para calcular la media aritmética de manera sencilla. La función =PROMEDIO en Excel, por ejemplo, permite calcular rápidamente el promedio de un rango de celdas.
Calculadoras Científicas
Para conjuntos de datos más pequeños, las calculadoras científicas ofrecen funciones básicas para calcular la media aritmética de forma manual.
Conclusiones
La media aritmética es una herramienta estadística esencial que ofrece una manera simple y directa de resumir conjuntos de datos cuantitativos. Aunque es una medida poderosa, su uso debe ser considerado cuidadosamente, especialmente en casos donde los datos contienen valores extremos o distribuciones sesgadas. A pesar de sus limitaciones, la media aritmética sigue siendo una medida de tendencia central fundamental en una amplia gama de disciplinas, desde las ciencias sociales hasta la ingeniería y las finanzas. Su aplicabilidad universal y su facilidad de uso garantizan que continuará siendo una herramienta estadística crucial en el análisis de datos y la toma de decisiones en el futuro.
Referencias
- Mendenhall, W., Beaver, R. J., & Beaver, B. M. (2013). «Introduction to Probability and Statistics.» Brooks/Cole, Cengage Learning.
- DeGroot, M. H., & Schervish, M. J. (2012). «Probability and Statistics.» Pearson Education.
- Triola, M. F. (2014). «Elementary Statistics.» Pearson Education.
- Anderson, D. R., Sweeney, D. J., & Williams, T. A. (2011). «Statistics for Business and Economics.» South-Western, Cengage Learning.
- Newbold, P., Carlson, W. L., & Thorne, B. (2013). «Statistics for Business and Economics.» Pearson Education.
Más Informaciones
El término «media aritmética» o «promedio aritmético» es una medida estadística fundamental utilizada para resumir un conjunto de datos numéricos en un solo valor representativo. Se calcula sumando todos los valores en un conjunto y dividiendo la suma por el número total de elementos en ese conjunto. Esta medida es ampliamente utilizada en diversos campos, desde la estadística y las matemáticas hasta la economía, la física y la ingeniería, entre otros.
La fórmula para calcular la media aritmética de un conjunto de datos es:
Donde son los valores individuales en el conjunto de datos, y es el número total de valores en el conjunto.
Una de las principales características de la media aritmética es que es sensible a los valores atípicos o extremos en un conjunto de datos. Esto significa que incluso un solo valor muy alto o muy bajo puede afectar significativamente el valor de la media aritmética. Por ejemplo, si tienes un conjunto de datos de temperaturas diarias y un día registra una temperatura extremadamente alta, ese valor extremo aumentará la media aritmética, lo que puede distorsionar la comprensión general de la distribución de las temperaturas.
Otra característica importante de la media aritmética es que es fácil de entender e interpretar. Es el concepto de promedio más básico y se utiliza ampliamente en situaciones cotidianas. Por ejemplo, cuando las personas hablan sobre el promedio de edad de una población o el promedio de calificaciones en un examen, están refiriéndose a la media aritmética.
Sin embargo, a pesar de su simplicidad y popularidad, la media aritmética tiene sus limitaciones. Una de las principales limitaciones es que puede no ser representativa de la distribución real de los datos, especialmente cuando los datos están sesgados o no siguen una distribución normal. En tales casos, otras medidas de tendencia central, como la mediana o la moda, pueden ser más apropiadas.
La mediana, por ejemplo, es otro tipo de medida de tendencia central que representa el valor central de un conjunto de datos cuando estos se ordenan en orden ascendente o descendente. A diferencia de la media aritmética, la mediana no se ve afectada por los valores extremos en el conjunto de datos, lo que la hace más robusta en presencia de valores atípicos.
Por otro lado, la moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Mientras que la media aritmética y la mediana se centran en torno a los valores numéricos, la moda se centra en la frecuencia de los valores. Es especialmente útil cuando se trabaja con datos categóricos o discretos, como colores, nombres o categorías.
En resumen, la media aritmética es una medida estadística fundamental utilizada para resumir conjuntos de datos numéricos. Aunque es sensible a los valores atípicos y puede ser fácil de entender e interpretar, tiene sus limitaciones y puede no ser representativa de la distribución real de los datos en todas las situaciones. Por lo tanto, es importante considerar otras medidas de tendencia central, como la mediana y la moda, para obtener una comprensión más completa de los datos.
Claro, profundicemos en algunos aspectos adicionales relacionados con la media aritmética.
1. Aplicaciones en la vida cotidiana:
La media aritmética se utiliza en una amplia variedad de situaciones en la vida cotidiana. Por ejemplo, en el ámbito financiero, se puede calcular la media aritmética de los ingresos mensuales de una persona o el promedio de gastos en un determinado período de tiempo para gestionar adecuadamente las finanzas personales. En el ámbito educativo, los profesores pueden utilizar la media aritmética para calcular las calificaciones de los estudiantes en un curso. Además, en el ámbito empresarial, las empresas suelen calcular la media aritmética de las ventas o los costos para analizar el rendimiento financiero.
2. Relación con otras medidas estadísticas:
La media aritmética es solo una de varias medidas de tendencia central utilizadas en estadística. Además de la mediana y la moda, mencionadas anteriormente, también existen medidas como la media ponderada y la media geométrica. La media ponderada asigna pesos diferentes a cada valor en el conjunto de datos, lo que significa que algunos valores pueden tener más influencia en la media final que otros. La media geométrica se utiliza comúnmente en situaciones donde los valores se multiplican entre sí, como en el cálculo de tasas de crecimiento o rendimientos financieros.
3. Propiedades matemáticas:
La media aritmética presenta varias propiedades matemáticas importantes. Por ejemplo, si todos los valores en un conjunto de datos se multiplican por un factor constante, la media aritmética también se multiplicará por ese mismo factor. Además, la suma de las desviaciones de cada valor con respecto a la media aritmética es siempre igual a cero, lo que significa que la media aritmética representa un punto de equilibrio en el conjunto de datos. Estas propiedades son fundamentales en el análisis estadístico y proporcionan una comprensión más profunda de la naturaleza de la media aritmética.
4. Limitaciones y precauciones:
Es importante tener en cuenta que la media aritmética puede no ser la medida más adecuada en todas las situaciones. Por ejemplo, en conjuntos de datos con valores extremadamente dispersos o sesgados, la media aritmética puede no ser representativa de la verdadera distribución de los datos. En tales casos, puede ser más apropiado utilizar medidas de tendencia central alternativas, como la mediana o la moda. Además, al interpretar la media aritmética, es fundamental considerar el contexto de los datos y estar atento a la posibilidad de valores atípicos que puedan distorsionar la interpretación de los resultados.
5. Interpretación en distribuciones asimétricas:
En distribuciones asimétricas, donde los datos están sesgados hacia un extremo, la media aritmética puede estar influenciada significativamente por los valores extremos. Por ejemplo, en una distribución de ingresos, donde la mayoría de las personas tienen ingresos bajos pero hay algunas personas con ingresos extremadamente altos, la media aritmética puede ser mucho mayor que la mediana, que representaría mejor el ingreso típico de la población. Por lo tanto, al interpretar la media aritmética en distribuciones asimétricas, es importante considerar el sesgo y la posible influencia de los valores extremos.
En resumen, la media aritmética es una herramienta estadística fundamental con una amplia gama de aplicaciones en diversos campos. Sin embargo, es importante comprender sus limitaciones y utilizarla de manera adecuada, considerando el contexto de los datos y teniendo en cuenta otras medidas de tendencia central cuando sea necesario.