Línea Recta: Concepto y Aplicaciones

Introducción

La línea recta es una de las formas geométricas más fundamentales y esenciales en matemáticas y geometría. Su simplicidad y propiedades únicas la hacen indispensable en una amplia variedad de disciplinas, desde la arquitectura hasta la física y la ingeniería. Este artículo explorará en profundidad el concepto de línea recta, sus propiedades, ecuaciones, y aplicaciones prácticas en diversos campos.

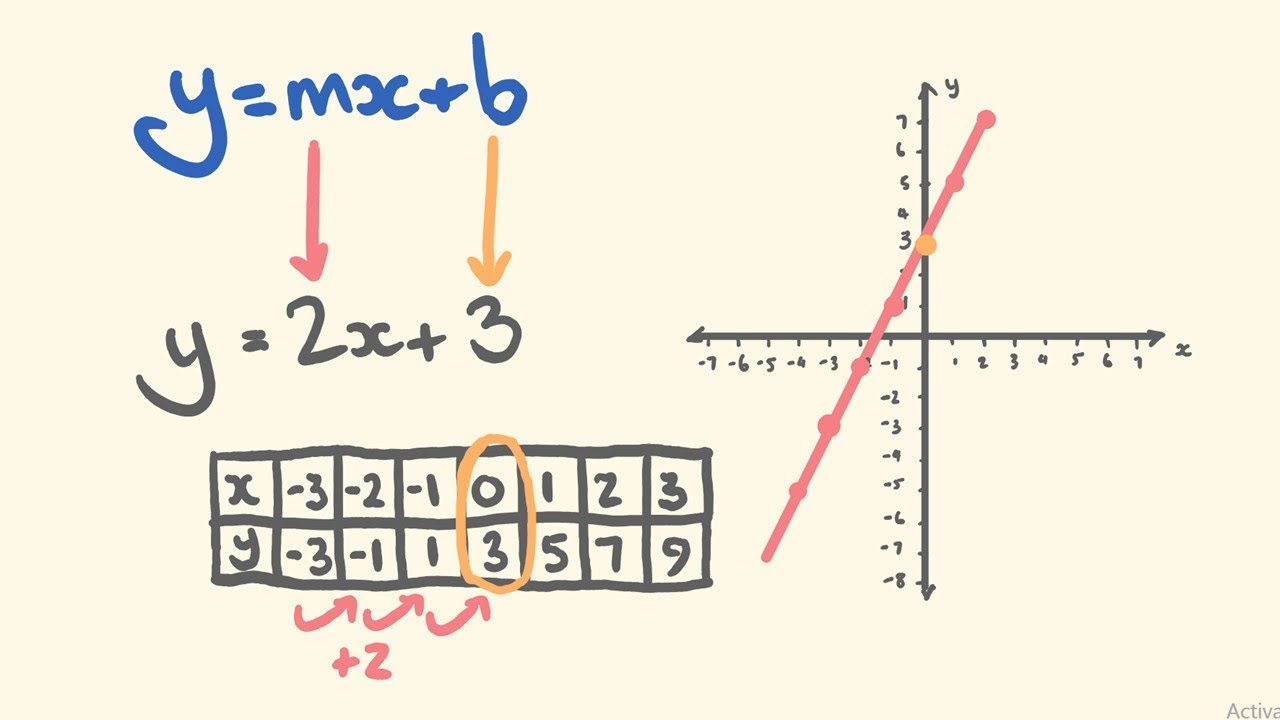
Concepto de Línea Recta

Definición

Una línea recta se define como una sucesión continua de puntos que se extiende infinitamente en ambas direcciones sin curvarse. En términos matemáticos, una línea recta en un plano bidimensional se puede representar por una ecuación lineal de la forma:

$y = mx + b$

donde $m$ es la pendiente de la línea y $b$ es la intersección con el eje $y$.

Propiedades de la Línea Recta

Las propiedades más importantes de una línea recta incluyen:

1. Infinita Extensión: Una línea recta no tiene ni principio ni fin, se extiende infinitamente en ambas direcciones.
2. Unicidad: Por dos puntos cualesquiera en un plano, solo puede pasar una única línea recta.
3. Pendiente: La pendiente de una línea recta indica su inclinación y se calcula como la relación entre el cambio en $y$ y el cambio en $x$.
4. Ángulos: La línea recta puede formar ángulos con los ejes de coordenadas, y estos ángulos determinan la dirección de la línea.

Ecuaciones de la Línea Recta

Ecuación General

La ecuación general de una línea recta en el plano $xy$ se puede expresar como:

$Ax + By + C = 0$

donde $A$, $B$ y $C$ son constantes.

Ecuación Punto-Pendiente

La ecuación punto-pendiente se utiliza cuando se conoce la pendiente de la línea y un punto por el cual pasa. Se expresa como:

$y – y_1 = m(x – x_1)$

donde $(x_1, y_1)$ es un punto en la línea y $m$ es la pendiente.

Ecuación Pendiente-Intersección

Esta es la forma más comúnmente utilizada y se expresa como:

$y = mx + b$

donde $m$ es la pendiente y $b$ es la intersección con el eje $y$.

Ecuación Paramétrica

La ecuación paramétrica de una línea recta es útil en aplicaciones de física y ingeniería y se expresa en términos de un parámetro $t$:

$x = x_0 + at$
$y = y_0 + bt$

donde $(x_0, y_0)$ es un punto en la línea y $a$, $b$ son direcciones.

Aplicaciones de la Línea Recta

En Geometría y Trigonometría

• División de Ángulos: Las líneas rectas se utilizan para dividir ángulos y encontrar ángulos complementarios y suplementarios.
• Construcción de Figuras: Las líneas rectas son esenciales para la construcción de figuras geométricas básicas como triángulos, cuadriláteros y polígonos.

En Álgebra y Cálculo

• Representación Gráfica: Las ecuaciones lineales se representan gráficamente como líneas rectas en el plano cartesiano.
• Sistemas de Ecuaciones: Las soluciones de sistemas de ecuaciones lineales corresponden a las intersecciones de líneas rectas.

En Física

• Movimiento Rectilíneo Uniforme: La trayectoria de un objeto que se mueve con velocidad constante es una línea recta.
• Óptica: En la óptica geométrica, la luz se modela como líneas rectas llamadas rayos.

En Ingeniería

• Diseño Estructural: Las líneas rectas son fundamentales en el diseño de estructuras como edificios y puentes, proporcionando estabilidad y resistencia.
• Gráficos y Modelos: En ingeniería, los gráficos de tensión-deformación y otros modelos de comportamiento lineal se representan mediante líneas rectas.

En Arquitectura

• Diseño y Planificación: Las líneas rectas se utilizan en la planificación de edificios y espacios para crear diseños estéticamente agradables y funcionales.
• Proporciones y Simetría: Las propiedades de las líneas rectas se utilizan para asegurar proporciones correctas y simetría en los diseños arquitectónicos.

En Informática y Programación

• Gráficos Computacionales: Los algoritmos de dibujo de líneas, como el algoritmo de Bresenham, son esenciales para la representación de gráficos en computadoras.
• Modelado y Simulación: En la simulación de trayectorias y movimientos, las líneas rectas son utilizadas para simplificar los cálculos.

En Economía y Finanzas

• Análisis de Tendencias: Las líneas de tendencia en gráficos financieros son líneas rectas que ayudan a identificar la dirección de los movimientos del mercado.
• Modelos Lineales: Los modelos económicos y financieros a menudo utilizan ecuaciones lineales para predecir comportamientos y resultados.

En Educación

• Enseñanza de Matemáticas: La comprensión de las líneas rectas es fundamental en la educación matemática, desde la escuela primaria hasta la universidad.
• Resolución de Problemas: Las líneas rectas se utilizan en la resolución de problemas geométricos y algebraicos en contextos educativos.

Conclusión

La línea recta, con su simplicidad y versatilidad, es una herramienta indispensable en muchas áreas del conocimiento. Desde la representación gráfica de ecuaciones hasta la planificación de estructuras arquitectónicas, su aplicación es amplia y variada. Comprender sus propiedades y ecuaciones permite a estudiantes, profesionales y académicos aprovechar al máximo esta forma geométrica fundamental en sus respectivos campos.

Referencias

1. Euclides. (300 a.C.). Los Elementos.
2. Stewart, J. (2015). Cálculo: Conceptos y Contextos. Cengage Learning.
3. Tipler, P. A., & Mosca, G. (2008). Física para Ciencias e Ingeniería. Reverté.
4. Sullivan, M., & Sullivan, M. (2012). Precalculus: Concepts Through Functions, A Right Triangle Approach to Trigonometry. Pearson.
5. Larson, R., & Edwards, B. H. (2013). Calculus of a Single Variable. Cengage Learning.
6. Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of Physics. Wiley.