La geometría euclidiana, también conocida simplemente como geometría, es una rama fundamental de las matemáticas que se centra en el estudio de las propiedades y relaciones de los objetos geométricos en el plano y en el espacio tridimensional utilizando los postulados y axiomas formulados por el matemático griego Euclides en su obra «Elementos», escrita alrededor del siglo III a.C. Este enfoque geométrico se ha mantenido como uno de los pilares fundamentales de la matemática durante más de dos milenios y ha sido una fuente de inspiración y desarrollo para numerosas áreas de la ciencia y la ingeniería.


Uno de los aspectos distintivos de la geometría euclidiana es su énfasis en la estructura axiomática, donde los conceptos fundamentales, como los puntos, las líneas, los planos y las figuras geométricas, se definen en términos de axiomas básicos que no requieren demostración y se aceptan como verdaderos por definición. Estos axiomas proporcionan el marco sobre el cual se construye toda la teoría geométrica, y cualquier proposición o teorema derivado de ellos debe ser demostrado rigurosamente utilizando las reglas de la lógica y la deducción.
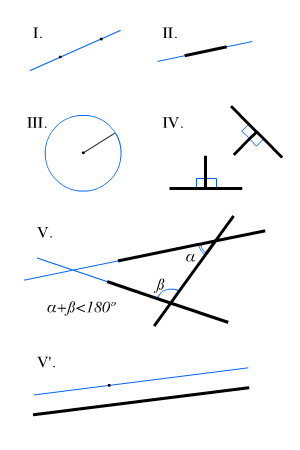
Los cinco postulados de Euclides, que forman la base de la geometría euclidiana, son los siguientes:
- Postulado de la recta y los puntos: Dados dos puntos distintos, existe exactamente una recta que los contiene.
- Postulado del segmento de línea: Dados dos puntos, es posible trazar un segmento de línea que los une.
- Postulado del extensión infinita: Una línea recta puede extenderse indefinidamente en ambas direcciones.
- Postulado del ángulo recto: Dados una línea recta y un punto no perteneciente a ella, existe exactamente una línea recta perpendicular a la dada que pasa por el punto.
- Postulado de los paralelos: Por un punto exterior a una recta dada, solo pasa una recta paralela a la dada.
A partir de estos postulados, se derivan una serie de teoremas y propiedades geométricas que constituyen el cuerpo principal de la geometría euclidiana. Estos incluyen resultados sobre la congruencia y semejanza de figuras, la medida de ángulos y longitudes de segmentos, la clasificación de polígonos y sólidos, entre otros.
La geometría euclidiana también abarca áreas como la geometría del plano y la geometría del espacio tridimensional. En la geometría del plano, se estudian las propiedades de los objetos geométricos como puntos, líneas, ángulos y polígonos dentro de un plano bidimensional. Mientras tanto, la geometría del espacio tridimensional extiende estos conceptos al espacio tridimensional, donde se consideran objetos geométricos como planos, poliedros, esferas y cilindros.
A lo largo de la historia, la geometría euclidiana ha sido fundamental en el desarrollo de numerosas disciplinas científicas y tecnológicas. Desde la antigüedad, ha sido utilizada en la astronomía para describir las órbitas planetarias, en la arquitectura para diseñar estructuras y edificios, y en la ingeniería para resolver problemas de diseño y construcción. Además, ha proporcionado la base conceptual para el desarrollo de otras ramas de la geometría, como la geometría analítica, la geometría proyectiva y la geometría diferencial.
En la era moderna, el surgimiento de la geometría no euclidiana, que se aparta de los postulados de Euclides y explora geometrías con propiedades diferentes, ha ampliado aún más el alcance y la relevancia de la geometría como disciplina matemática. Sin embargo, la geometría euclidiana sigue siendo un campo de estudio fundamental y esencial en la formación matemática básica, proporcionando herramientas y conceptos fundamentales para el desarrollo de la teoría matemática y su aplicación en diversas áreas del conocimiento humano.
Más Informaciones

Por supuesto, profundicemos en algunos aspectos adicionales de la geometría euclidiana para comprender mejor su importancia y aplicaciones.
1. Estructura Axiomática:
La geometría euclidiana se caracteriza por su estructura axiomática rigurosa. Los axiomas son proposiciones básicas que se aceptan como verdaderas sin necesidad de demostración. A partir de estos axiomas, se deducen teoremas y propiedades geométricas mediante la aplicación de reglas lógicas.
2. Elementos de Euclides:
La obra «Elementos» de Euclides, escrita alrededor del 300 a.C., es una de las obras más influyentes en la historia de las matemáticas. Este texto establece los fundamentos de la geometría euclidiana y organiza sus resultados en un sistema deductivo coherente. Contiene trece libros que cubren diversos temas, como la teoría de números, la teoría de proporciones y la geometría plana y del espacio.
3. Teoremas Fundamentales:
La geometría euclidiana abarca una amplia variedad de teoremas y resultados fundamentales. Algunos de los teoremas más conocidos incluyen el Teorema de Pitágoras, que establece la relación entre los lados de un triángulo rectángulo, y el Teorema de Tales, que describe propiedades de las proporciones en figuras geométricas similares.
4. Geometría del Plano y del Espacio:
La geometría euclidiana se divide en dos ramas principales: la geometría del plano y la geometría del espacio tridimensional. En la geometría del plano, se estudian las propiedades y relaciones de los objetos geométricos en un plano bidimensional, como líneas, ángulos y polígonos. En la geometría del espacio tridimensional, se extienden estos conceptos al espacio tridimensional, donde se consideran objetos como planos, poliedros, esferas y cilindros.
5. Aplicaciones Históricas y Modernas:
A lo largo de la historia, la geometría euclidiana ha tenido una gran influencia en diversas áreas. En la antigüedad, fue fundamental en campos como la astronomía, la arquitectura y la ingeniería. En la era moderna, la geometría euclidiana sigue siendo relevante en campos como la física, la informática, la robótica y la ingeniería civil, donde se utiliza en el diseño y análisis de estructuras y sistemas.
6. Desarrollos Posteriores:
A pesar de su importancia histórica, la geometría euclidiana ha sido objeto de críticas y desarrollos posteriores. En el siglo XIX, se descubrieron geometrías no euclidianas, que contradecían algunos de los postulados de Euclides y llevaban a conclusiones geométricas diferentes. Estas geometrías, desarrolladas por matemáticos como Nikolái Lobachevski, János Bolyai y Bernhard Riemann, ampliaron el alcance de la geometría y condujeron al desarrollo de la geometría diferencial y la geometría algebraica.
7. Significado Filosófico:
La geometría euclidiana también ha tenido un impacto en la filosofía y la epistemología. Su estructura axiomática y su enfoque en la demostración rigurosa de teoremas han influido en la forma en que se concibe la verdad y el conocimiento en la tradición occidental. Además, el estudio de la geometría euclidiana ha llevado a reflexiones sobre la naturaleza del espacio, el tiempo y la realidad física.
En resumen, la geometría euclidiana es mucho más que un conjunto de teoremas y propiedades geométricas; es una disciplina matemática que ha influido profundamente en el pensamiento humano y ha sido fundamental en el desarrollo de la ciencia y la tecnología a lo largo de la historia. Su estructura axiomática, su riqueza teórica y sus aplicaciones prácticas la convierten en un tema central en la formación matemática y en el estudio de la naturaleza y el universo.

