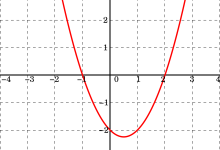
Funciones Lineales: Propiedades y Aplicaciones

Introducción a las Funciones Lineales

Las funciones lineales son uno de los conceptos fundamentales en matemáticas y se utilizan en múltiples disciplinas, desde la física hasta la economía. Estas funciones se caracterizan por su simplicidad y por representar relaciones proporcionales entre dos variables. En términos matemáticos, una función lineal tiene la forma:

$y = mx + b$

Donde:

$y$ es la variable dependiente,
$x$ es la variable independiente,
$m$ es la pendiente de la recta, que indica la tasa de cambio de $y$ con respecto a $x$ ,
$b$ es el término constante o intercepto, que indica dónde la recta cruza el eje $y$ .

En este artículo se analizarán en profundidad las propiedades de las funciones lineales, sus aplicaciones en diversos campos y cómo su simplicidad facilita la modelización de fenómenos en el mundo real.

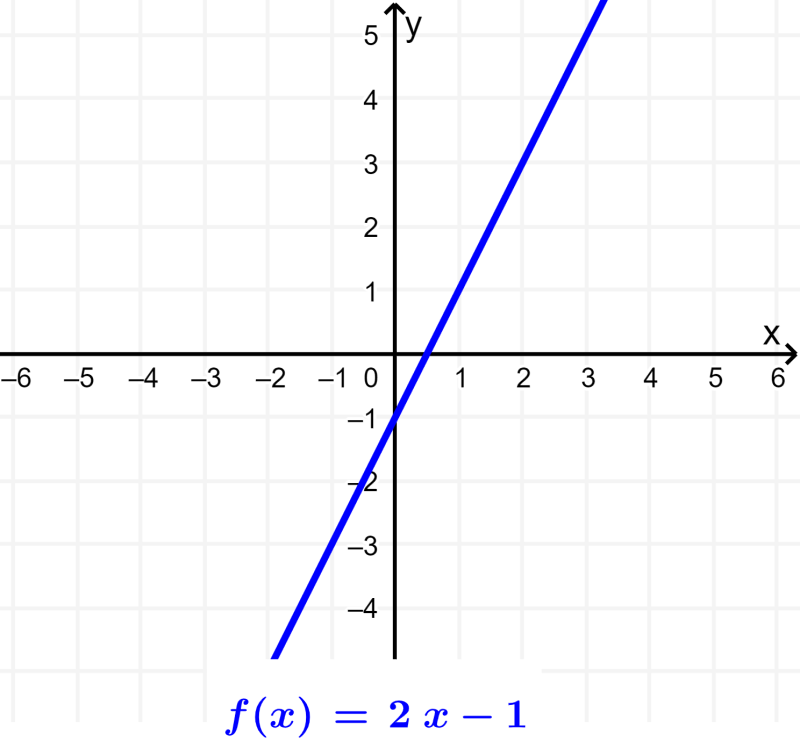
Propiedades de las Funciones Lineales

Las funciones lineales tienen varias propiedades matemáticas que las hacen útiles para modelar relaciones directas. Entre estas propiedades destacan las siguientes:

1. Pendiente Constante

Una de las características más notables de una función lineal es que la pendiente $m$ es constante. Esto significa que la tasa de cambio entre $y$ y $x$ es la misma en cualquier punto de la función. Matemáticamente, la pendiente se puede calcular como:

$m = \frac{\Delta y}{\Delta x}$

Esto implica que la relación entre los dos valores es constante, lo que facilita el análisis y predicción de tendencias en los datos.

2. Intercepto

El intercepto, o valor de $b$ , es el punto en el que la recta cruza el eje $y$ cuando $x = 0$ . Este valor es importante porque define la posición de la recta en el gráfico sin afectar la pendiente. Cambiar el valor de $b$ mueve la recta hacia arriba o hacia abajo sin alterar su inclinación.

3. Proporcionalidad Directa

En las funciones lineales, los cambios en la variable independiente $x$ producen cambios proporcionales en la variable dependiente $y$ . Esta propiedad es útil para modelar fenómenos donde un incremento en una cantidad está relacionado directamente con un incremento en otra cantidad. Por ejemplo, si en una empresa el ingreso es directamente proporcional a la cantidad de productos vendidos, se puede usar una función lineal para modelar esta relación.

4. Simetría

Las funciones lineales poseen una simetría particular cuando la pendiente es positiva o negativa. Si $m$ es positivo, la función es creciente, lo que indica que a medida que $x$ aumenta, $y$ también lo hace. Si $m$ es negativo, la función es decreciente, lo que significa que $y$ disminuye a medida que $x$ aumenta. Esta característica es esencial para la interpretación de fenómenos que involucran relaciones inversas o directas entre dos variables.

5. Dominio y Rango

El dominio de una función lineal es el conjunto de todos los posibles valores de $x$ , que en general es $\mathbb{R}$ (todos los números reales). Del mismo modo, el rango es el conjunto de todos los posibles valores de $y$ , que también es $\mathbb{R}$ . Esto significa que una función lineal puede tomar cualquier valor en el plano cartesiano, lo que la hace especialmente útil para modelar fenómenos continuos.

6. Comportamiento Asintótico

Las funciones lineales no tienen asintotas. Una asintota es una línea a la cual una curva se aproxima pero nunca toca. Dado que las funciones lineales son rectas, no presentan un comportamiento asintótico, lo que las diferencia de otras funciones más complejas, como las exponenciales o racionales.

7. Gráfico: Rectas en el Plano

El gráfico de una función lineal es siempre una recta. La forma de esta recta depende de la pendiente $m$ y el intercepto $b$ . Si $m = 0$ , la función es una recta horizontal, lo que indica que $y$ es constante sin importar el valor de $x$ . Si $m > 0$ , la recta tiene una pendiente positiva, mientras que si $m < 0$ , la pendiente es negativa. El término $b$ simplemente determina en qué punto la recta cruza el eje $y$ .

8. Inversibilidad

Las funciones lineales de la forma $y = mx + b$ (donde $m \neq 0$ ) son funciones invertibles, lo que significa que para cada valor de $y$ existe un valor único de $x$ tal que $y = mx + b$ . La inversa de una función lineal tiene la forma:

$x = \frac{y – b}{m}$

Esto es particularmente útil en aplicaciones donde se necesita resolver para $x$ en función de $y$ .

Aplicaciones de las Funciones Lineales

Las funciones lineales son omnipresentes en muchas áreas de estudio y en aplicaciones del mundo real. A continuación se examinan algunas de sus aplicaciones más importantes en campos como la economía, la ingeniería, la física y las ciencias sociales.

1. Economía y Finanzas

En economía, las funciones lineales se utilizan para modelar una amplia gama de fenómenos. Un ejemplo común es el cálculo de los ingresos de una empresa. Si una empresa vende un producto a un precio fijo $p$ por unidad, y $x$ representa el número de unidades vendidas, los ingresos totales $y$ se pueden modelar mediante una función lineal:

$y = px$

Además, las funciones lineales se emplean en el análisis de costos, donde los costos fijos y variables de producción pueden expresarse mediante una ecuación lineal. El costo total $C$ puede representarse como:

$C = C_f + C_v x$

Donde $C_f$ es el costo fijo y $C_v$ es el costo variable por unidad producida.

2. Física

En física, las funciones lineales se utilizan para describir fenómenos como el movimiento rectilíneo uniforme, donde la velocidad de un objeto es constante. En este caso, la distancia recorrida $d$ es una función lineal del tiempo $t$ :

$d = vt + d_0$

Donde $v$ es la velocidad constante y $d_0$ es la distancia inicial.

Otro ejemplo es la ley de Hooke en mecánica de sólidos, que establece que la fuerza ejercida por un resorte es directamente proporcional a su extensión:

$F = kx$

Donde $F$ es la fuerza, $k$ es la constante del resorte y $x$ es la extensión.

3. Ingeniería

En ingeniería, las funciones lineales son esenciales para modelar sistemas eléctricos y mecánicos simples. Por ejemplo, en la ley de Ohm, la corriente eléctrica $I$ que fluye a través de un conductor es directamente proporcional al voltaje $V$ aplicado:

$V = IR$

Donde $R$ es la resistencia del conductor.

Este tipo de relaciones lineales son fundamentales en el diseño de circuitos eléctricos y otros sistemas técnicos.

4. Ciencias Sociales

En las ciencias sociales, las funciones lineales se utilizan para modelar relaciones entre variables sociales y económicas. Por ejemplo, se pueden usar para analizar cómo el ingreso de una persona influye en su gasto. Si se asume una relación lineal entre el ingreso $I$ y el gasto $G$ , entonces el modelo puede ser:

$G = mI + b$

Donde $m$ representa la propensión marginal a consumir, y $b$ es el gasto autónomo (gasto cuando el ingreso es cero).

5. Geometría y Trigonometría

Las funciones lineales también tienen aplicaciones en la geometría. Por ejemplo, la ecuación de una recta en el plano cartesiano se puede expresar en términos de una función lineal:

$y = mx + b$

Este tipo de ecuaciones se utilizan para estudiar intersecciones de líneas, encontrar ángulos entre líneas, y resolver problemas relacionados con pendientes y distancias.

Conclusión

Las funciones lineales son una herramienta matemática poderosa y versátil, con aplicaciones en diversos campos. Su simplicidad y su capacidad para modelar relaciones proporcionales entre variables las convierten en una de las formas más útiles de función en matemáticas aplicadas. Desde la economía hasta la física, pasando por las ciencias sociales y la ingeniería, las funciones lineales proporcionan una forma eficiente de representar y analizar datos, permitiendo la predicción y el control de fenómenos complejos en el mundo real.

A medida que el conocimiento de las matemáticas continúa expandiéndose, el estudio de las funciones lineales sigue siendo fundamental tanto en la teoría como en la práctica.

Más Informaciones

Las funciones lineales son un concepto fundamental en el ámbito de las matemáticas, específicamente en el campo del álgebra y el análisis matemático. Una función lineal es una función que tiene la forma básica de una línea recta cuando se representa gráficamente en un plano cartesiano. Estas funciones tienen propiedades distintivas que las hacen importantes en diversos contextos matemáticos y aplicaciones prácticas.

Una función lineal se define matemáticamente como $f(x) = mx + b$ , donde $m$ y $b$ son constantes reales. El coeficiente $m$ representa la pendiente de la línea, mientras que $b$ es la ordenada al origen, es decir, el valor de $f(x)$ cuando $x = 0$ . Estos dos parámetros determinan completamente la función lineal y su comportamiento.

Entre las propiedades más destacadas de las funciones lineales se encuentran:

Propiedad de Linealidad: Como su nombre indica, las funciones lineales cumplen con la propiedad de linealidad. Esto significa que la función satisface dos condiciones fundamentales: la aditividad y la homogeneidad. La aditividad implica que $f(x+y) = f(x) + f(y)$ , mientras que la homogeneidad implica que $f(kx) = kf(x)$ , donde $k$ es una constante real.
Representación Gráfica: Gráficamente, una función lineal se representa por una línea recta en el plano cartesiano. La pendiente de la línea indica la tasa de cambio de la función, es decir, cuánto cambia $y$ respecto a $x$ . Por otro lado, la ordenada al origen determina dónde corta la línea al eje $y$ cuando $x = 0$ .
Invariancia Bajo Traslaciones y Escalaciones: Las funciones lineales son invariantes bajo traslaciones y escalaciones. Esto significa que si trasladamos o escalamos la gráfica de una función lineal, sigue manteniendo su forma básica de línea recta. La pendiente y la ordenada al origen pueden cambiar, pero la esencia de la función permanece igual.
Comportamiento Monótono: Las funciones lineales son monótonas, lo que significa que siempre se incrementan o siempre se decrementan a medida que $x$ aumenta. La dirección del incremento o decremento depende del signo de la pendiente. Si la pendiente es positiva, la función aumenta; si es negativa, la función disminuye.
Intersección con los Ejes Coordenados: La intersección de una función lineal con los ejes coordenados proporciona información valiosa sobre su comportamiento. La intersección con el eje $y$ se conoce como la ordenada al origen ( $b$ ), mientras que la intersección con el eje $x$ se puede encontrar resolviendo $f(x) = 0$ , lo que da el valor de $x$ donde la función corta el eje $x$ .
Comportamiento Asintótico: En el límite cuando $x$ tiende a infinito, una función lineal se comporta de manera asintótica. Esto significa que se aproxima indefinidamente a la recta, pero nunca la alcanza. La pendiente de la función determina la dirección y la inclinación de la asintota.
Operaciones con Funciones Lineales: Las funciones lineales son cerradas bajo operaciones de suma y multiplicación por escalares. Esto significa que la suma de dos funciones lineales y el producto de una función lineal por un escalar también son funciones lineales.
Aplicaciones Prácticas: Las funciones lineales tienen numerosas aplicaciones en diversos campos, como la física, la economía, la ingeniería y la informática. Por ejemplo, en economía, se utilizan para modelar relaciones de proporcionalidad en problemas de oferta y demanda. En física, describen el movimiento rectilíneo uniforme, entre otros fenómenos.

En resumen, las funciones lineales son objetos matemáticos de gran importancia debido a sus propiedades distintivas y su amplia gama de aplicaciones prácticas. Su estudio no solo es fundamental en matemáticas puras, sino también en la resolución de problemas en diversos campos científicos y tecnológicos.

Por supuesto, profundicemos aún más en las propiedades y características de las funciones lineales:

Ecuación General de una Función Lineal: Además de la forma $f(x) = mx + b$ , las funciones lineales también pueden expresarse en la forma general $ax + by + c = 0$ , donde $a$ , $b$ , y $c$ son constantes reales y $a$ y $b$ no son ambos cero. Esta forma general se utiliza comúnmente en geometría analítica para describir líneas en el plano cartesiano.
Pendiente y Ángulo de Inclinación: La pendiente de una función lineal $m$ se calcula como el cambio en $y$ dividido por el cambio en $x$ . Matemáticamente, $m = \frac{\Delta y}{\Delta x}$ , donde $\Delta y$ es la variación en la coordenada $y$ y $\Delta x$ es la variación en la coordenada $x$ . El ángulo de inclinación de la función lineal respecto al eje $x$ se puede encontrar utilizando la tangente inversa de la pendiente.
Paralelismo y Perpendicularidad: Dos funciones lineales son paralelas si y solo si tienen la misma pendiente. Por otro lado, dos funciones lineales son perpendiculares si el producto de sus pendientes es -1. Estas relaciones son fundamentales en geometría analítica y se utilizan para resolver problemas de intersección y ortogonalidad.
Recta de Regresión: En estadística, la recta de regresión lineal es una herramienta utilizada para modelar la relación entre dos variables. Se ajusta a los datos de tal manera que minimiza la suma de los cuadrados de las desviaciones verticales entre los puntos de datos y la recta. La ecuación de la recta de regresión es una función lineal que representa la mejor aproximación lineal a los datos.
Matrices y Transformaciones Lineales: En álgebra lineal, las funciones lineales pueden representarse mediante matrices y vectores. Cada función lineal puede asociarse con una matriz, y la multiplicación de esta matriz por un vector produce una transformación lineal del vector original. Este enfoque es fundamental en áreas como la geometría computacional y el procesamiento de imágenes.
Ecuaciones Paramétricas de una Recta: Otra forma de representar una función lineal es mediante ecuaciones paramétricas. En este enfoque, la función lineal se describe en términos de un parámetro $t$ , y las coordenadas $x$ y $y$ se expresan en función de $t$ . Este enfoque es útil para visualizar la trayectoria de un objeto en movimiento en el espacio.
Interpretación Gráfica de la Pendiente y la Ordenada al Origen: La pendiente de una función lineal indica la inclinación de la línea con respecto al eje $x$ , mientras que la ordenada al origen representa el punto donde la línea corta el eje $y$ . Estas características tienen interpretaciones gráficas significativas y proporcionan información sobre el comportamiento de la función en el plano cartesiano.
Interpretación Económica de las Funciones Lineales: En economía, las funciones lineales se utilizan para modelar relaciones de proporcionalidad en diversos contextos. Por ejemplo, en el análisis de costos y beneficios, las funciones lineales pueden representar el costo total como una función del volumen de producción, o los ingresos como una función del precio de venta y la cantidad vendida.
Resolución de Problemas de Optimización: Las funciones lineales se utilizan en la resolución de problemas de optimización en los que se busca maximizar o minimizar una función sujeta a ciertas restricciones lineales. Estos problemas son comunes en áreas como la ingeniería, la economía y la logística, y se resuelven mediante técnicas como la programación lineal.
Aplicaciones en Ingeniería Eléctrica y Electrónica: En ingeniería eléctrica y electrónica, las funciones lineales se utilizan para modelar la relación entre la corriente y el voltaje en circuitos lineales, así como para analizar sistemas de control y comunicaciones. Las ecuaciones de Kirchhoff y las leyes de Ohm son ejemplos de aplicaciones de funciones lineales en este campo.

En conclusión, las funciones lineales son una herramienta fundamental en matemáticas y tienen una amplia gama de aplicaciones en diversas áreas, desde la geometría analítica y la estadística hasta la ingeniería y la economía. Su estudio proporciona una base sólida para comprender conceptos más avanzados y resolver problemas en el mundo real.

Last Updated: 26/09/2024